Magic Squares
|
Period: Approximately 2,200 BCE ~
Magic squares are a type of mathematical puzzle in which numbers are placed in individual square cells to form the shape of a larger square where the sum of all the values in the rows, columns, and main diagonals are equal. If the number of cells on any given side is represented by n, then the values placed inside the various cells are the numbers 1 through n2. Additionally, magic squares with n rows and columns are said to be of the nth-order. |
The first historical accounts of magic squares come from ancient China. The original purpose of magic squares may have had more to do with divination than mathematics. The first mention of magic squares is from a manuscript dating around 2,200 BCE, the time of Emperor Yu.
|
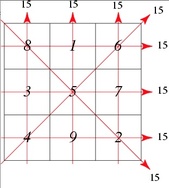
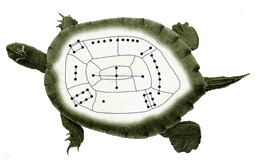
Legend has it that the river Lo would flood and destroy the crops and land, so people would try to appease the river god by offering it sacrifices. Every time the river flooded, a turtle would emerge and walk around the sacrifice. The number of sacrifices required was discovered by a child that noticed a particular pattern on the turtle’s back, which contained a shape similar to a three-by-three magic square in the form of dots. Each row, column, and diagonal held the same sum of 15, and therefore that is the number of sacrifices that the river god was believed to have desired.
|
Although the first accounts of magic squares come from China, magic squares were also developed by people in other regions, such as the Mayan Indians and the Hasua people of Africa. The oldest documented fourth-order magic square found is dated to the eleventh or twelfth century from Khajuraho, India. In the thirteenth century, a prominent Chinese mathematician named Yang Hui developed two magic squares each of orders four through eight, and one each of orders nine and ten.
Magic Squares in ArtMagic squares have shown up in a few famous pieces of art. In 1514, the German mathematician and artist Albrecht Durer included a fourth-degree magic square in his work entitled Melancholia. The magic square appears in the upper right-hand corner of the artwork, and “1514,” the year in which the work was made, is created out of two adjacent cells on the bottom of the magic square. Additionally, there is an untraditional fourth-order magic square in the Sagrada Familia church in Barcelona, Spain, which is modified by repeating some of the numbers, in which each row, column, and diagonal add up to 33, the age that Jesus is said to have died according to the bible.
|
More Magic Square Facts
In 1693, Bernard Frenicle de Bessy, an amateur French mathematician and magic square researcher posthumously published the 880 different fourth-order magic squares. The total possible magic squares that can be created from the numbers 1, 4, 9, 16, and 25 are 1, 0, 1, 880, and 275,305,224, respectively. The more numbers to make magic squares from, the more difficult they become to complete. The number of possible original magic squares of an arbitrary order is a problem yet to be solved.
In addition to traditional magic squares, there are a number of variations with slightly different rules that apply to the total sums of the different rows, columns, and diagonals. First, it should be noted that the number that each row, column, and main diagonal add up to in a regular magic square is called the magic constant. The formula for finding the magic constant is (n(n2+1))/2.
If one or both of the main diagonals do not add up to the magic constant, it is called a semimagic square. If not just the main diagonals but all the diagonals add up to the magic constant by wrapping around the square, it is called a panmagic square. Multiplying the integers in each cell by a constant, or adding each integer to a constant is another way to create more types of magic squares. A number of other varieties exist as well. There are even extensions of magic squares in higher dimensions, including magic tesseracts, which are four-dimensional cubes that contain numbers 1 through n4 that exhibit the equivalent properties of magic squares in four dimensions.
In addition to traditional magic squares, there are a number of variations with slightly different rules that apply to the total sums of the different rows, columns, and diagonals. First, it should be noted that the number that each row, column, and main diagonal add up to in a regular magic square is called the magic constant. The formula for finding the magic constant is (n(n2+1))/2.
If one or both of the main diagonals do not add up to the magic constant, it is called a semimagic square. If not just the main diagonals but all the diagonals add up to the magic constant by wrapping around the square, it is called a panmagic square. Multiplying the integers in each cell by a constant, or adding each integer to a constant is another way to create more types of magic squares. A number of other varieties exist as well. There are even extensions of magic squares in higher dimensions, including magic tesseracts, which are four-dimensional cubes that contain numbers 1 through n4 that exhibit the equivalent properties of magic squares in four dimensions.
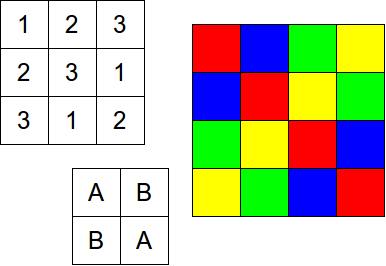
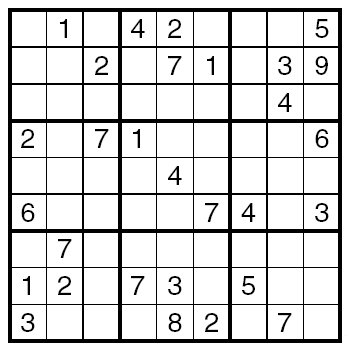
Magic Squares in CultureAlthough magic squares may have started out with divination purposes, their mathematical properties and the joy and challenge of constructing them have intrigued people for thousands of years. Sudoku, a popular math puzzle commonly found in newspapers, puzzle books, or digital applications, was inspired by a variation on magic squares devised by Leonhard Euler in the 18th century called Latin squares. In this variation, only numbers 1 through n are used, and each number only appears once in each row and column.
|
|
In the mid-nineteenth century, an amateur puzzle enthusiast in New York named Palmer Chapman made a physical model of a fourth-order magic square but left out one piece so that the individual cells could slide around. This was known as the 15 Puzzle, because it had 15 pieces. In the 1970’s, Erno Rubrik, a Hungarian designer, was attempting to recreate the 15 puzzle in three dimensions when he came up with the Rubik’s Cube. These hit items are a testament to the fascination that people around the world have with puzzles, and it’s no wonder that magic squares are still being created by people and used in math classes as well as math tournaments today.
|
References for this page
Bellos, A. (2011). Magic squares are given a whole new dimensions. Retrieved from http://www.guardian.co.uk/science/2011/apr/03/magic-squares-geomagic-lee-sallows
Boyer, C. B., Merzbach, U. C. (3rd Ed.) (2011). A history of mathematics. New Jersey: John Wiley & Sons, Inc.
Magic Squares: A Simple Webquest. (n.d.). History. Retrieved from http://plaza.ufl.edu/ufkelley/magic/history.htm
Mankiewicz, R. (2000). The story of mathematics. New Jersey: Princeton University Press.
Pickover, C. A. (2009). The math book: from pythagoras to the 57th dimension. New York/London: Sterling.
Smith, K., J. (12th Ed.) (2012). The nature of mathematics. United States of America: Brooks/Cole, Cengage Learning.
The On-line Encyclopedia of Integer Sequences. (2012). Number of different magic squares of order n that can be formed from the numbers 1, …, n^2. Retrieved from http://oeis.org/A006052
Weisstein, E., W. (n.d.). Magic square. Retrieved from http://mathworld.wolfram.com/MagicSquare.html
Boyer, C. B., Merzbach, U. C. (3rd Ed.) (2011). A history of mathematics. New Jersey: John Wiley & Sons, Inc.
Magic Squares: A Simple Webquest. (n.d.). History. Retrieved from http://plaza.ufl.edu/ufkelley/magic/history.htm
Mankiewicz, R. (2000). The story of mathematics. New Jersey: Princeton University Press.
Pickover, C. A. (2009). The math book: from pythagoras to the 57th dimension. New York/London: Sterling.
Smith, K., J. (12th Ed.) (2012). The nature of mathematics. United States of America: Brooks/Cole, Cengage Learning.
The On-line Encyclopedia of Integer Sequences. (2012). Number of different magic squares of order n that can be formed from the numbers 1, …, n^2. Retrieved from http://oeis.org/A006052
Weisstein, E., W. (n.d.). Magic square. Retrieved from http://mathworld.wolfram.com/MagicSquare.html
Author: Jonathan Sack (2012)